| Похожие рефераты | Скачать .docx | Скачать .pdf |
Реферат: Геометрические свойства равнобедренных треугольников
В. В. Богун
Предлагаемая статья, как следует из названия, посвящена изучению свойств равнобедренных треугольников, а также установлению взаимосвязей между данными треугольниками. Необходимость исследований назрела, в первую очередь, из-за частого применения в архитектуре равнобедренных треугольников как геометрических моделей отдельных фрагментов зданий и сооружений, а во-вторых, пополнения базы знаний в области элементарной геометрии.
Где же могут найти применение данные теоретические исследования? Прежде всего в педагогике как таковой, поскольку они существенно расширят кругозор школьников и студентов, изучающих элементарную геометрию, а также тригонометрию, поскольку работа находится на стыке двух разделов математики - элементарной геометрии и тригонометрии, причем их важность абсолютно равнозначна.
Существенными плюсами данных исследований являются следующие факты:
Возможность выхода на теорию стереометрической взаимосвязи между геометрическими фигурами, в частности, правильных четырехугольных пирамид;
Объяснение с помощью свойств равнобедренных треугольников и построенных на их основе правильных четырехугольных пирамид геометрических взаимосвязей между пирамидами Гизы в Египте (Хеопса, Хефрена и Микерина);
Последний факт должен вызвать особый интерес читательской аудитории к исследованиям, поскольку в отличие от всей геометрии в целом, представленной в популярных учебниках в большинстве случаев лишь в виде "голой" теории, мы имеем сочетание теоретических и практических аспектов.
Для простоты изложения материала внесем ряд определений:
Основная высота - высота равнобедренного треугольника, опущенная из вершины, являющейся точкой пересечения равных боковых сторон, на основание и соответственно пересекающей последнее в его середине.
Полуподобные равнобедренные треугольники - равнобедренные треугольники, для которых справедливо равенство углов при основании одного половинным углам между боковыми сторонами другого.
Половинноподобные равнобедренные треугольники - равнобедренные треугольники, равные углы при основании одного являются половинными углами при основании другого.
Теорема 1: Об отношении основной высоты равнобедренного треугольника к радиусу вписанной в него окружности
Отношение основной высоты равнобедренного треугольника к радиусу вписанной в него окружности равно алгебраической сумме единицы и величины, обратной по значению косинусу равных углов при основании.
Исходные данные:
Равнобедренный ∆ АВС (рис. 1); ВD = h основная высота, опущенная из вершины В на основание АС = 2 а; АВ = ВС = b боковые стороны треугольника; DО = КО = LО = r - радиус вписанной в ∆ АВС окружности, ВАС = ВСА = .
Доказать:
![]() (1)
(1)
Доказательство:
Формулы для вычисления площади ∆АВС:
S ∆АВС![]() .
.
S ∆АВС![]() .
.
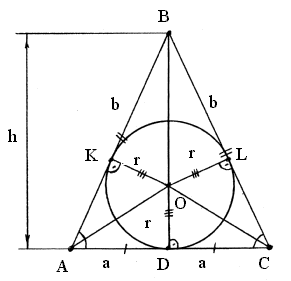
Рис. 1. Равнобедренный ∆ АВС с вписанной в него окружностью.
Получим:
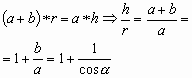 |
(1) |
Следствия из теоремы 1:
1.1.Отношение половины основания равнобедренного треугольника к радиусу вписанной в него окружности равно котангенсу половинного угла при основании:
Так как ![]() ,
,
а
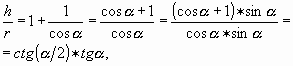
то
![]() . (2)
. (2)
Однако из курса геометрии известно, что центр вписанной в любой треугольник окружности лежит на пересечении биссектрис его углов.
1.2. Отношение боковой стороны равнобедренного треугольника к радиусу вписанной в него окружности равно отношению котангенса половинного угла при основании к косинусу полного угла при основании:
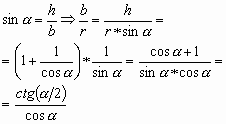 |
(3) |
1.3. В равнобедренном треугольнике отношение разницы между основной высотой и радиусом вписанной окружности к величине последнего равно отношению боковой стороны к половине основания или величине, обратной значению косинуса угла при основании:
![]() . (4)
. (4)
Теорема 2: Об отношении основной высоты равнобедренного треугольника к радиусу описанной вокруг него окружности
Отношение основной высоты равнобедренного треугольника к радиусу описанной вокруг него окружности равно удвоенному произведению квадрата синуса угла при основании или разнице единицы и косинуса двойного угла при основании:
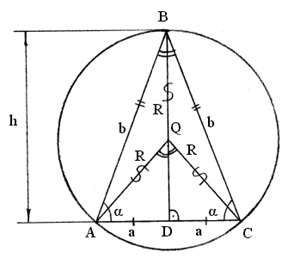
Рис. 2. Равнобедренный ∆ АВС с описанной вокруг него окружностью.
Исходные данные:
Равнобедренный ∆АВС (рис. 2); ВD = h - основная высота, опущенная из вершины В на основание АС = 2 а; АВ = ВС = b - боковые стороны треугольника; АQ = BQ = CQ = R - радиус описанной вокруг ∆АВС окружности, ВАС = ВСА = .
Доказать:
![]() (5)
(5)
Доказательство:
Формулы для вычисления площади ∆АВС:
S ∆АВС =![]()
S ∆АВС = ![]()
Получим: ![]()
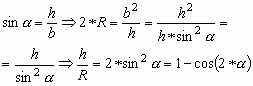 |
(5) |
Следствия из теоремы 2:
2.1. Отношение половины стороны основания равнобедренного треугольника к радиусу описанной вокруг него окружности равно синусу двойного угла при основании:
Так как
![]() ,
,
то
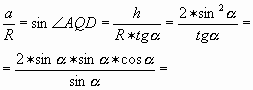
![]() (6)
(6)
Поскольку
![]() ,
,
то
![]()
2.2. Отношение боковой стороны к радиусу описанной окружности равно двум синусам углам при основании:
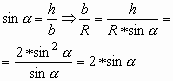 |
(7) |
2.3 В равнобедренном треугольнике отношение разницы между радиусом описанной окружности и основной высотой к величине первого равно косинусу двойного угла при основании:
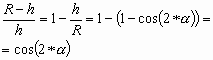 |
(8) |
Следствие из теорем 1 и 2:
В равнобедренном треугольнике отношение радиуса вписанной к радиусу описанной окружности равно произведению тангенса половинного угла при основании и синуса двойного угла при основании:
![]() (9)
(9)
В табл. 1 представлены взаимосвязи между линейными элементами равнобедренного треугольника (основная высота, половина основания, боковая сторона, радиусы вписанных и описанных окружностей), выражаемые через тригонометрические выражения равных углов при основании.
Таблица 1
Соотношения в равнобедренном треугольнике
| Y | ||||||
| a | b | h | R | R | ||
| XX | aa | 1 | ||||
| bb | 1 | |||||
| hh | 1 | |||||
| RR | 1 | |||||
| rr | 1 | |||||
В предлагаемых ниже двух теоремах рассмотрены взаимосвязи между вписанными и описанными окружностями двух равнобедренных треугольников, имеющих один общий элемент. В первой теореме данным субъектом является основная высота, во второй - сторона основания. Что же касается совпадения боковых сторон равнобедренных треугольников, то здесь получим равенство треугольников по двум сторонам и углу между ними.
Теорема 3: О равных углах равнобедренных треугольников
Если два равнобедренных треугольника построены на одной основной высоте и равные углы при основании одного равны углу между боковыми сторонами второго, то их центры вписанной и описанной окружностей соответственно совпадут.
Исходные данные:
Равнобедренные ∆АВС и ∆ЕBF c общей основной высотой ВD = h. DO 1 = r и ВО 2 = R - радиусы вписанной и описанной окружностей равнобедренных ∆АВС и ∆ЕBF соответственно.
ВАС = ВСА = EBF = ,
BEF = BFE = (рис. 3)
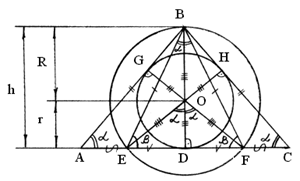
Рис. 3. Геометрическая интерпретация теоремы 3
Доказать:
h = R + r (10)
Доказательство:
Для равнобедренного ∆АВС:
![]()
Для равнобедренного ∆ЕBF:
![]()
По условию теоремы
ВАС = ВСА = EBF =
= , BEF = BFE = .
А так как
BEF = BFE =
![]() ,
,
получим:
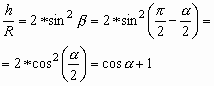
![]()
Если
![]() (10),
(10),
то ![]()
Действительно,
![]() ,
,
что и требовалось доказать.
Следствия из теоремы 3:
3.1. Если два равнобедренных треугольника построены на одной основной высоте и угол между боковыми сторонами одного равен углам при основании второго, то отношение соответствующих оснований равно разнице величины, обратной по значению косинусам равных углов при основании второго, и единице:
Так как
![]()
и
![]() ,
,
то
![]()
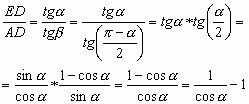 |
(11) |
3.2. Если два равнобедренных треугольника построены на одной основной высоте и равные углы при основании одного равны углу между боковыми сторонами второго, то отношение соответствующих боковых сторон равно половине величины, обратной по значению синусам равных углов при основании второго:
Поскольку
![]() и
и ![]() ,
,
то
![]() .
.
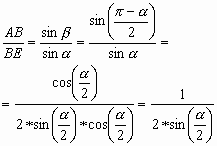 . . |
(12) |
Теорема 4: О половинных углах равнобедренных треугольников
Если два равнобедренных треугольника имеют общее основание и вершина, являющаяся пересечением боковых сторон первого, совпадает с центром вписанной во второй треугольник окружности, то центр описанной вокруг первого треугольника окружности лежит на пересечении перпендикуляров к боковым сторонам второго.
Исходные данные:
Равнобедренные ∆ АВС и ∆ АОС с общим основанием АС = 2 а, DO = r = H радиус вписанной окружности и высота равнобедренных ∆ АВС и ∆ AOC соответственно. ВАС = ВСА = , OAC = OCA = ![]() (рис. 4).
(рис. 4).
Доказать:
![]() (13)
(13)
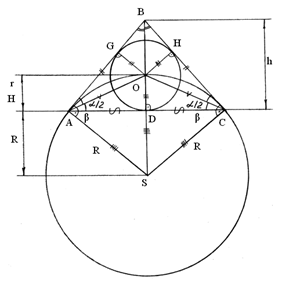
Рис. 4. Геометрическая интерпретация теоремы 4
Доказательство:
Исходя из рис. 4, получим следующую цепочку соотношений:
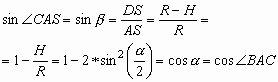
Тогда
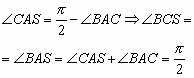 |
(13) |
При этом согласно определению равнобедренные ∆ АВС и ∆ АСS являются полуподобными, поскольку
![]()
и наоборот, а равнобедренные ∆АВС и ∆АОС являются половинноподобными, поскольку удовлетворяют определению:
ВАС = ВСА = , OAC = OCA = ![]()
Похожие рефераты:
Развитие логического мышления учащихся при решении задач на построение
Измерения геометрических величин в курсе геометрии 7-9 классов
Оценка периметра многоугольника заданного диаметра
Избранные теоремы геометрии тетраэдра
Методика изучения многогранников в школьном курсе стереометрии
Методика изучения объемов многогранников в курсе стереометрии